- given a non empty set A subset of R, The number x is called the upper bound of the set A if for every aЄA a is applied. the number A is said to be restricted to the top if it has an upper bound. the number x is said to be no upper bound of A if there is aЄA with a> x.
- the number x is called the lower bound of the set S if for every aЄA there is x≤a. A bundle is said to be limited to the bottom when it has a bottom. x is not a lower bound if there is aЄA with a<x.
- the number A is said to be limited if it has an upper & lower limit. In other words, a set A is said to be limited if there is such a number m> 0 that aЄA occurs −m≤a≤m.
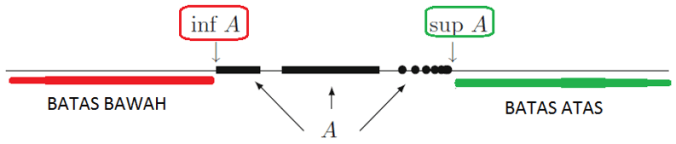
- batas bawah = infimum A (Lower bound)
- batas atas = supremum A (Upper bound)
- definition: number x is called infimum set A (inf A), if it satisfies the following conditions:
- x lower bound of set A
- if y is the lower bound of set A, then y≤x.
- Theorem: the number x = inf A when and only when
- x bottom bound A
- for every y> x there is aЄA with y> a
- Theorem: x = inf A when and only when
- x bottom bound A
- for every α> 0 there exists aЄA with x + α <a
- definition: number x is called supremum set A (sup A), if it satisfies the following conditions:
- x upper bound of set A
- if y is the upper bound of A, then y≥x
- Theorem: the number x = soup A when and only when
- x upper bound A
- for every y <x there is aЄA with y <a
- Theorem: the number x = soup A when and only when
- x upper bound A
- for every α> 0 there is aЄA with x − α <a
Pramitha Shafika Wicaksono Pages 